Mathe Geometrie Dreiecke, Vierecke, Kreise und andere ebene Figuren Flächen-, Umfangsberechnung und anderes zu ebenen Figuren Rätselaufgaben zu besonderen ebenen Figuren

Rätselaufgaben zu besonderen ebenen Figuren

Folgende Figur besteht aus Quadraten und einbeschriebenen Kreisen.Wie ist das Verhältnis des Radius des innersten Kreises zum Radius des äußersten Kreises?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras

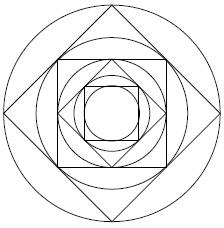
Inkreis und Umkreis eines Quadrates

Man bertrachtet zunächst die zwei äußersten Kreise und das äußerste Quadrat.

Der Durchmesser des Inkreises im Quadrat ist $a$ , also gilt für den Innkreisradius: $r_{i} = \frac{a}{2}$

Kreis Quadrat Inkreis Umkreis Satz des Pythagoras legacy geogebra formula

Den Umkreisradius kann man mit Hilfe des Satz des Pythagoras berechnen:

$r_{u}^{2} + r_{u}^{2}$	$=$	$a^{2}$
$2 r_{u}^{2}$	$=$	$a^{2}$	$: 2$
$r_{u}^{2}$	$=$	$\frac{a^{2}}{2}$	$\sqrt{}$
	↓	Wurzel ziehen
$r_{u}$	$=$	$\sqrt{\frac{a^{2}}{2}}$
	$=$	$\frac{a}{\sqrt{2}}$
	↓	Bruch erweitern
	$=$	$\frac{a \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}$
	$=$	$\frac{a}{{(\sqrt{2})}^{2}} \cdot \sqrt{2}$
	$=$	$\frac{a}{2} \cdot \sqrt{2}$

Wir betrachten zuerst allgemein ein Quadrat mit Umkreisradius $r_{u}$ und Inkreisradius $r_{i}$ .

Löse die eben erhaltene Formel $r_{u} = \frac{a}{2} \cdot \sqrt{2}$ nach der Seitenlänge a auf:

$r_{u}$	$=$	$\frac{a}{2} \sqrt{2}$	$\cdot 2$
$2 r_{u}$	$=$	$a \sqrt{2}$	$: \sqrt{2}$
$a$	$=$	$\frac{2 r_{u}}{\sqrt{2}}$

Nun kann a in die Formel für den Inkreisradius $r_{i} = \frac{a}{2}$ eingesetzt werden:

$r_{i}$	$=$	$\frac{\frac{2 r_{u}}{\sqrt{2}}}{2}$
	↓	Faktor 2 kürzen
	$=$	$\frac{r_{u}}{\sqrt{2}}$

Das heißt $r_{i}$ ist $\frac{1}{\sqrt{2}} \approx 0,71$ so groß wie $r_{u}$ .

Weil diese Zusammenhang allgemein gilt, gilt er natürlich auch für das äußerste Quadrat. Also:

r_{i 1} = \frac{r_{u 1}}{\sqrt{2}}

Nun betrachten wir das zweite Quadrat. Der Umkreis dieses Quadrats ist der Inkreis des äußersten Quadrats. Also gilt:

r_{i 1} = r_{u 2}

Mit dem allgemeinen Zusammenhang zwischen In- und Umkreisradius erhalten wir:

r_{i 2} = \frac{r_{u 2}}{\sqrt{2}} = \frac{r_{i 1}}{\sqrt{2}}

Setze jetzt $r_{i 1} = \frac{r_{u 1}}{\sqrt{2}}$ ein und vereinfache:

\begin{aligned} r_{i 2} & = \frac{\frac{r_{u 1}}{\sqrt{2}}}{\sqrt{2}} \\ = \frac{r_{u 1}}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2} \end{aligned}

Der Umkreis des dritten Quadrats ist der Inkreis des zweiten Quadrats. Also gilt:

r_{u 3} = r_{i 2} = \frac{r_{u 1}}{2}

Aber auch der allgemeine Zusammenhang zwischen In- und Umkreisradius glit in diesem Quadrat:

r_{i 3} = \frac{r_{u 3}}{\sqrt{2}}

Setze $r_{u 3} = \frac{r_{u 1}}{2}$ ein und vereinfache:

\begin{aligned} r_{i 3} & = \frac{\frac{r_{u 1}}{2}}{\sqrt{2}} \\ = \frac{r_{u 1}}{2} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \sqrt{2}} \end{aligned}

Auch beim vierten Quadrat ist der Umkreis der Inkreis des dritten Quadrats. Damit ergibt sich:

r_{u 4} = r_{i 3} = \frac{r_{u 1}}{2 \sqrt{2}}

Mit dem allgemeinen Zusammenhang zwischen In- und Umkreisradius folgt:

r_{i 4} = \frac{r_{u 4}}{\sqrt{2}}

Setze $r_{u 4} = \frac{r_{u 1}}{2 \sqrt{2}}$ ein und vereinfache:

\begin{aligned} r_{i 4} & = \frac{\frac{r_{u 1}}{2 \sqrt{2}}}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \sqrt{2}} \cdot \frac{1}{\sqrt{2}} \\ = \frac{r_{u 1}}{2 \cdot \sqrt{2} \cdot \sqrt{2}} \\ = \frac{r_{u 1}}{4} \end{aligned}

Das Verhältnis des Radius des innersten Kreises zum Radius des äußersten Kreis beträgt also 1:4.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org